Graph Traversals in C++

Graph traversals in the form of Depth-First-Search (DFS) and Breadth-First-Search (BFS) are one of the most fundamental algorithms in computer science. As the use of these algorithms plays an essential role in tasks such as cycle-detecting, path-finding, and topological sorting. For that reason, it is important to know how to implement a simple generic version of these functions.

The first point to consider before implementing a graph traversal algorithm is to identify what type of graph we want to traverse. To select a graph we have to ask ourselves if we want the graph to be directed or undirected? Will the graph be disconnected? Will it support cycles? In the case of this blog post, I decided to use an undirected graph. What this means is that the traversal algorithms may need slight modifications depending on the type of graph being used; nevertheless, the fundamental structure of the algorithm will remain the same.

The undirected graph presented in this example will use an adjacency list representation. The graph is implemented using a hash map of key-value pairs between each vertex and the list of neighbor vertices around it. The implementation of the undirected graph is presented below:

Graph Implementation:

template<typename VertexType>
using UndirectedGraph = std::unordered_map<VertexType, std::vector<VertexType>>;

template<typename VertexType>
void addEdge(UndirectedGraph<VertexType>& undirected_graph, 
    const VertexType& source, const VertexType& destination)
{
    undirected_graph[source].push_back(destination);
    undirected_graph[destination].push_back(source);
}

Now that we have established an implementation for the graph, we can start thinking about the design of the traversals. In the case of graphs, the options for traversals are Depth-First-Search(DFS) and Breadth-First-Search(BFS). DFS is characterized by starting from a given vertex and then following a path until it ends, then it backtracks to the next possible path following the same procedure until the whole graph is traversed. In the case of BFS, the traversal begins at any selected vertex from where we begin to visit the neighbor vertices at the same depth level, and then move onto each level subsequently until the graph is fully traversed. A graphical visualization of both types of traversals in a tree graph is presented below:

Breadth First Search (BFS) Visualization

Depth First Search (DFS) Visualization

In regards to the implementation details of DFS and BFS, there are various commonalities shared between both algorithms. The main one being the use of a set to keep track of the visited nodes to prevent the traversal from being stuck in a cycle. The key difference between them is the use of a different data structure to process the order of each vertex. For DFS a stack is used as the Last-In-First-Out (LIFO) order serves the purpose of traversing down a path and then backtrack as the traversal reaches its end. While in BFS a queue is used as its First-In-First-Out structure helps navigate each vertex on a level by level basis. The generic implementation for both traversals is presented below:

BFS Implementation:

template<typename VertexType, typename Function = std::invoke_result<void(VertexType&)>::type>
void BFS(const UndirectedGraph<VertexType>& undirected_graph, VertexType current_vertex,
    const Function& process_vertex_function)
{
    std::queue<VertexType> queue;
    queue.push(current_vertex);

    std::unordered_set<VertexType> visited_vertices;
    visited_vertices.insert(current_vertex);

    while (!queue.empty())
    {
        current_vertex = queue.front();
        queue.pop();

        process_vertex_function(current_vertex);
        
        for (auto neighbor_vertex : undirected_graph.at(current_vertex))
        {
            if (!visited_vertices.count(neighbor_vertex))
            {
                visited_vertices.insert(neighbor_vertex);
                queue.push(neighbor_vertex);
            }
        }
    }
}

DFS Implementation:

template<typename VertexType, typename Function = std::invoke_result<void(VertexType&)>::type>
void DFS(const UndirectedGraph<VertexType>& undirected_graph, VertexType current_vertex, 
    const Function& process_vertex_function)
{
    std::stack<VertexType> stack;
    stack.push(current_vertex);

    std::unordered_set<VertexType> visited_vertices;

    while (!stack.empty())
    {
        current_vertex = stack.top();
        stack.pop();

        if (visited_vertices.count(current_vertex))
        {
            continue;
        }

        visited_vertices.insert(current_vertex);

        process_vertex_function(current_vertex);

        for (auto neighbor_vertex : undirected_graph.at(current_vertex))
        {
            stack.push(neighbor_vertex);
        }
    }
}

Usage Example:

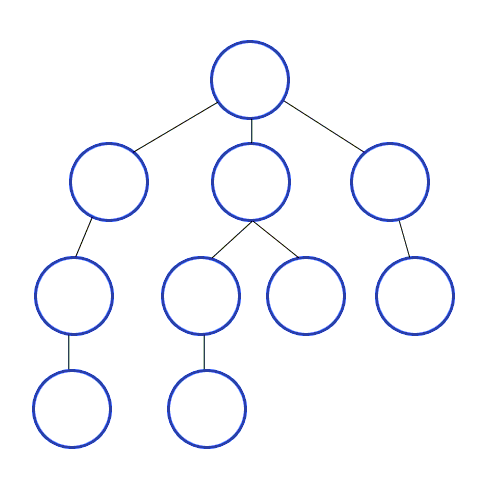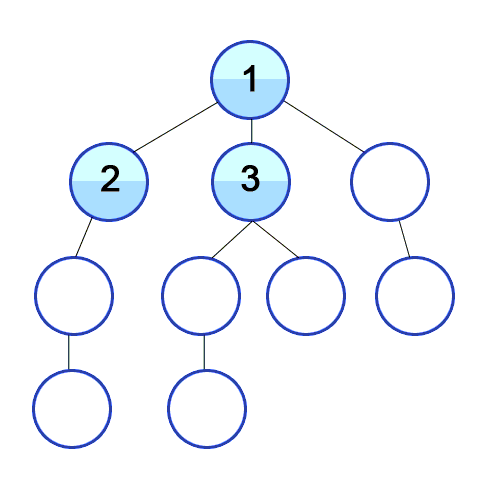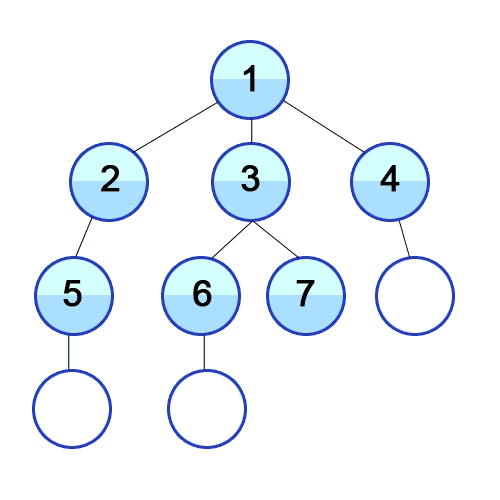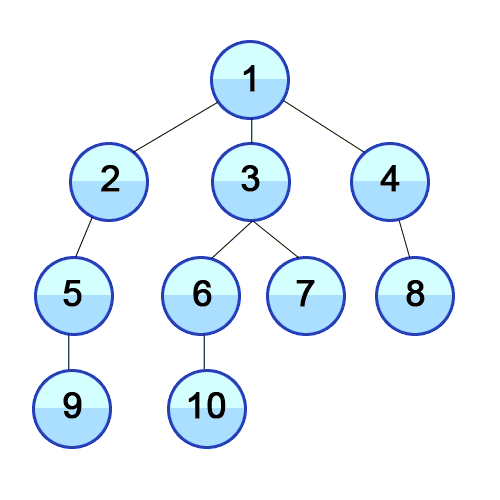
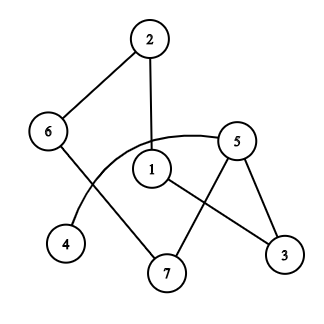
int main()
{
    UndirectedGraph<int> graph;

    addEdge(graph, 1, 2);
    addEdge(graph, 2, 6);
    addEdge(graph, 1, 3);
    addEdge(graph, 3, 5);
    addEdge(graph, 4, 5);
    addEdge(graph, 5, 7);
    addEdge(graph, 6, 7);
    
    auto print_vertex = [](auto& vertex) 
    { std::cout << vertex << ' '; };

    std::cout << "BFS: ";
    BFS(graph, 1, print_vertex);

    std::cout << '\n';

    std::cout << "DFS: ";
    DFS(graph, 1, print_vertex);
}

Graph Used in Example

Output:
BFS: 1 2 3 6 5 7 4
DFS: 1 3 5 7 6 2 4

Conclusion

Breadth-First-Search and Depth-First-Search traversals have a wide range of applications in many algorithms, thus it is essential to understand their theory and implementations. While there are various kinds of graphs with unique properties, the general structure of DFS and BFS remains very similar. Lastly, if you are interested in additional graph algorithms and more robust implementations make sure to take a look at The Boost Graph Library.

Source Code

How to Generate Permutations of a String in C++

Generating all possible permutations of a set of elements is generally done by using recursive methods. Therefore, to generate the permutations of a string we are going to use backtracking as a way to incrementally build a permutation and stop as soon as we have used every possible character in the string. The method implemented below uses this idea to solve the permutation problem:

Backtracking Method #1 (Using std::swap)

void add_permutation1(std::vector<std::string>& permutations, std::string& str, std::size_t curr_index)
{
    if (curr_index == str.size() - 1)
    {
        permutations.push_back(str);
        return;
    }

    for (auto j = curr_index; j < str.size(); ++j)
    {
        std::swap(str[curr_index], str[j]);

        add_permutation1(permutations, str, curr_index + 1);

        //Restoring string to its original state
        std::swap(str[curr_index], str[j]);
    }
}

std::vector<std::string> get_permutations1(const std::string& str)
{
    std::vector<std::string> permutations;
    
    auto str_cpy = str;
  
    add_permutation1(permutations, str_cpy, 0);

    return permutations;
}

The next backtracking method uses a similar concept with the difference of using a reduced subset with the leftover characters instead of keeping track of the current index is presented below:

Backtracking Methods #2 (Using std::rotate)

void add_permutation2(std::vector<std::string>& permutations, std::string str, 
    const std::string curr_permutation& = "")
{
    if (str.empty())
    {
        permutations.push_back(curr_permutation);
        return;
    }

    for (auto c : str)
    {
        add_permutation2(permutations, str.substr(1), curr_permutation + str[0]);

        //Rotating string one index to the left
        std::rotate(str.begin(), str.begin() + 1, str.end());
    }
}

std::vector<std::string> get_permutations2(const std::string& str)
{
    std::vector<std::string> permutations;

    add_permutation2(permutations, str);

    return permutations;
}

Fortunately, it’s not necessary to deal with any of the details of the recursive code as the C++ STL provides the function std::next_permutation that transforms the range of elements to its next permutation based on lexicographical order.

STL Method (using std::next_permutation)

std::vector<std::string> get_permutations3(const std::string& str)
{
    std::vector<std::string> permutations;

    auto str_cpy = str;

    do{
        permutations.push_back(str_cpy);
    } while (std::next_permutation(str_cpy.begin(), str_cpy.end()));
    //Stops as soon as the new permutation is lexicographically smaller than the old one (comes back to original state)
  
    return permutations;
}

Conclusion

Backtracking offers a simple and effective way of generating all possible permutations of a string. If you don’t want to deal with the implementation details of generating permutations then its possible to use functions such as std::next_permutation or std::prev_permutation to get the job done.

Source Code

How to Binary Search in C++

Binary Search is a very useful algorithm whenever we are dealing with an already sorted group of elements. If we take a look at the C++ STL we find a function called std::binary_search that implements this algorithm but upon further research, we learn that it only tells us if the search value is present in the container, rather than returning an iterator of the value found. So how do we implement a generic binary search function that finds the location of the value that we want to search? A simple implementation based on traditional binary search would look something like this:

Implementation #1

template<typename Iter, typename Val, typename Comp = std::less<>>
Iter binary_search1(Iter begin, Iter end, const Val& search_val, Comp comp = {})
{
    auto original_end = end; //saving end to return when value is not found

    while (begin != end)
    {
        auto mid = begin + (end - begin) / 2;

        if (search_val == *mid) 
        {
            return mid;
        }
        else if (!comp(search_val, *mid)) //search_val > mid
        {
            begin = mid + 1;
        }
        else //search_val < mid
        {
            end = mid;
        }
    }

    return original_end;
} 

While the first implementation follows the common steps needed to perform binary search it, is not taking advantage of C++ library features that could help shorten and simplify the code. For that reason, the second implementation presented below makes use of std::lower_bound: a function from the algorithm header that returns an iterator to the first element that is greater than or equal to the search value, or an iterator to the end of the container if no value was found.

Implementation #2 (Using lower_bound)

template<typename Iter, typename Val, typename Comp = std::less<>>
Iter binary_search2(Iter begin, Iter end, const Val& search_val, Comp comp = {})
{
    auto found_itr = std::lower_bound(begin, end, search_val, comp);

    if (found_itr != end && !comp(search_val, *found_itr)) //search_val >= found_itr
    {
        return found_itr;
    }

    return end;
}

Clearly, the use of std::lower_bound makes the implementation of binary search a rather straightforward task as it takes away from most of the error-prone details that are present in the algorithm.

Conclusion

Since C++ doesn’t provide a proper binary search function that returns the iterator of the value to be found, it is needed to write additional code to provide a generic and useful solution. Luckily, the use of std::lower_bound eases the implementation of the algorithm and allows us to enjoy the benefits of working with a sorted container.

Source Code

How to Find the Kth Largest Element in an Array

The most obvious way to find the Kth largest element in an array would be to sort the array in descending order and then access its element at the index k - 1. However, the shortcoming of this approach comes from the fact that it doesn’t solve this problem in the most optimal way with regards to time complexity.

Brute-Force Solution (Time Complexity: O(nlogn), Space Complexity: O(1))

int Kth_largest(const std::vector<int>& array, int k)
{
   std::sort(array.rbegin(), array.rend());
  
   return array[k - 1];
}

To advance towards a more optimal solution we need to make use of another data structure that provides us with better time complexity guarantees. A priority queue is an excellent tool for this kind of improvement as it allows us to compare at most K elements instead of the whole array whenever we are sorting as we traverse through the array.

Min-Heap Priority Queue Solution (Time Complexity: O(nlogk), Space Complexity: O(k))

int Kth_largest(const std::vector<int>& array, int k)
{
   std::priority_queue<int, std::vector<int>, std::greater<int>> queue;
  
   for(auto val : array)
   {
      queue.push(val);
     
      if(queue.size() > k)
      {
          queue.pop();
      }
   }
  
    return queue.top();
}

This solution is a little more verbose than the first one, but it is still very simple and useful when time efficiency is of concern. Moreover, the previous implementation is also adaptable to the Kth smallest element problem by replacing the min-heap queue with a max-heap queue. Fortunately, the C++ STL provides an in-built function called nth_element that is implemented with partial sorting using introspective selection to offer an excellent linear average time complexity with the only downside of the rare case of a bad partition that leads to a worst possible time complexity of O(nlogn).

Nth Element Solution (Avg Time Complexity: O(n), Worst Time Complexity: O(nlogn), Space Complexity: O(1))

int Kth_largest(const std::vector<int>& array, int k)
{
   std::nth_element(array.begin(), array.begin() + k - 1, array.end(), std::greater<int>());
  
   return array[k - 1];
}

Conclusion

It is necessary to divert from the standard sorting of an array to find an optimal time efficient solution to the Kth largest element problem. Priority queues and more specialized partial sorting algorithms provide an excellent alternative to solving this issue.

Source Code

How to Iteratively Traverse a Binary Tree

Binary tree traversals are generally done in a recursive manner because this type of problem tends to be simplified by such methods. Nevertheless, the key advantage gained by using an iterative approach is the fact that the traversal will not run out of stack space. Moreover, there is always something to learn when solving a problem in an alternative way.

Below are the iterative implementations of the different types of traversals that can be done with a binary tree alongside an explanation of how they work:

Pre-Order Traversal

void print_pre_order(TreeNode* root)
{
    if (!root)
    {
        return;
    }
        
    std::stack<TreeNode*> stack;
    stack.push(root);

    while (!stack.empty())
    {
        auto* node = stack.top();
        stack.pop();

        std::cout << node->val << ' ';

        if (node->right)
        {
            stack.push(node->right);
        }    
        if (node->left)
        {
            stack.push(node->left);
        }    
    }
}

Pre-Order traversal consists of traversing the left subtree before advancing to the right subtree. This behavior is achieved through the use of a Last In First Out (LIFO) data structure like a stack. The insertion of the right nodes occurs before the left nodes in order to make sure that the left nodes will be the first ones to be accessed.

Post-Order Traversal

void print_post_order(TreeNode* root)
{
    if (!root)
    {
        return
    }
       
    std::stack<TreeNode*> stack, out_stack;
    stack.push(root);

    while (!stack.empty())
    {
        auto* node = stack.top();
        stack.pop();

        out_stack.push(node);

        if (node->left)
        {
            stack.push(node->left);
        }
        if (node->right)
        {
            stack.push(node->right);
        }
    }

    while (!out_stack.empty())
    {
        auto* node = out_stack.top();
        out_stack.pop();

        std::cout << node->val << ' ';
    }
}

The Post-Order iterative tree traversal algorithm is slightly more complex than the Pre-Order one because the solution uses two stacks. The first stack gets the reverse Post-Order traversal in a similar manner to the algorithm used for the Pre-Order traversal with the only difference that the left node is inserted before the right one. The purpose of the second stack is to get the reverse of the first stack and in turn get the proper Post-Order traversal.

In-Order Traversal

void print_in_order(TreeNode* root)
{
    std::stack<TreeNode*> stack;
    auto* curr = root;

    while (!stack.empty() || curr)
    {
        if (curr)
        {
            stack.push(curr);
            curr = curr->left;
        }
        else
        {
            curr = stack.top();
            stack.pop();

            std::cout << curr->val << ' ';

            curr = curr->right;
        }
    }
}

In-Order traversal involves a current pointer pivot that will traverse the leftmost part of the tree and insert itself to a stack until it reaches a null value. If the current pointer is null and the stack is not empty then the pivot pointer moves towards the rightward node from the node at the top of the stack, otherwise, the traversal stops as the whole tree has been accessed.

Level-Order Traversal

void print_level_order(TreeNode* root)
{
    if (!root)
    {
        return;
    }
        
    std::queue<TreeNode*> queue;
    queue.push(root);

    while (!queue.empty())
    {
        const auto LEVEL_SIZE = queue.size();

        for (std::size_t i = 0; i < LEVEL_SIZE; ++i)
        {
            auto* node = queue.front();
            queue.pop();

            std::cout << node->val << ' ';

            if (node->left)
            {
                queue.push(node->left);
            }
            if (node->right)
            {
                queue.push(node->right);
            }
        }
    }
}

The Level-Order traversal algorithm is different from all the previous methods mentioned in the fact that it uses a First In First Out (FIFO) data structure in the form of a queue. The way it works consists of accessing every node in a single level and then insert the left and right child nodes to use them in the next cycle of iteration for each upcoming level. As a side note, it is not necessary to include the for loop to iterate through every level of the tree as the queue itself will handle this behavior; nevertheless, this is added to make a distinction for every level of the tree that is being accessed.

Conclusion

Undoubtedly, the iterative approach of traversing a binary tree traversal is a more verbose and complex solution when compared to its recursive counterpart. Despite that, implementing another way of traversing a tree adds a level of comprehension for key data structures such as stacks and queues, as well as, include the benefit of not having to worry about running out of stack space.

Source Code

How to Format a String in C++

String formatting is a common and useful operation that is regularly used in most programming languages. Unfortunately, the formatting solution offered in the C++ Standard Library lacks simplicity and intuitiveness. For that reason, implementing a C-style “printf” type function for string formatting can be a worthy investment as it offers an advantage in terms of convenience over C++ I/O manipulators.

The implementation below makes use of several C++11 features that improve readability and safety concerns that would exist in older legacy code. The most notable one being the variadic template parameter pack that acts as a wrapper around the variadic function used in C-style “printf” methods.

template<typename... Args>
std::string format_string(const std::string& format, Args... args)
{
    const auto size = std::snprintf(nullptr, 0, format.c_str(), args...) + 1;
    const auto buffer = std::make_unique<char[]>(size);

    std::snprintf(buffer.get(), size, format.c_str(), args...);

    return std::string(buffer.get(), buffer.get() + size - 1);
}

Here’s a quick rundown of what is happening in this function:

1. The size of the char array is determined by getting the return value from std::snprintf. (Note: plus one is added to this value to make room for the null terminator at the end of the array)

2. A new char array is allocated through the use of a unique pointer to not worry about manually deleting this memory again.

3. std::snprintf is used to write the formatted string into the char array.

4. A new string is created from the char array buffer and then returned.

While this function seems to get the job done, there is still one more point missing to fully support C++ specific types. More specifically, this method doesn’t work whenever a std::string object is passed as part of its argument list. To fix this issue there needs to be an additional check to convert a std::string object into a “const char*” so that it gets forwarded as a parameter for std::snprintf. The complete implementation considering this aspect is shown below (Note: this solution uses C++17 features):

template<typename T>
auto convert(T&& t)
{
    if constexpr (std::is_same<std::remove_cv_t<std::remove_reference_t<T>>, std::string>::value)
    {
        return std::forward<T>(t).c_str();
    }
    else
    {
        return std::forward<T>(t);
    }
}

template<typename... Args>
std::string format_string_internal(const std::string& format, Args&& ... args)
{
    const auto size = std::snprintf(nullptr, 0, format.c_str(), std::forward<Args>(args)...) + 1;
    const auto buffer = std::make_unique<char[]>(size);

    std::snprintf(buffer.get(), size, format.c_str(), std::forward<Args>(args)...);

    return std::string(buffer.get(), buffer.get() + size - 1);
}

template<typename... Args>
std::string format_string(const std::string& format, Args&& ... args)
{
    return format_string_internal(format, convert(std::forward<Args>(args))...);
}

Now this solution may seem like a lot more complex than the previous one, but in reality, there is not a lot that has changed. The most noticeable difference is the inclusion of the “convert” function that checks at compile-time if the parameter passed is a string, and if it is then it returns the C-string given by the “c_str()” method, otherwise, it returns the type itself. Moreover, an additional format function is added to make sure the user does not have to explicitly call the “convert” method whenever formatting a string. Lastly, the use of std::forward is included to ensure perfect forwarding takes place.

Conclusion

C-style “printf” functions provide a simpler and more intuitive interface compared to the C++ standard solution of using I/O manipulators. Hence, the previous implementation for a string formatting function offers a great alternative from what can currently be done using C++ streams. As a side note, libraries like fmt and boost::format also provide great solutions to string formatting needs.

Source Code

How to Create a Random String in C++

Generating a random string in C++ is a simple task that can be easily achieved by the use of rand(); however, this method is not recommended because rand() lacks a distribution engine and the quality of its implementation leaves more to be desired. To combat this issue, the C++ Standard Library provides a set of functions from the Random header that allows users to generate random numbers from well-defined engines and distributions. The implementation of the function that generates a random string will make use of three key features present in the facilities of the Random header.

The elements used being:

• std::random_device: uniformly distributed random number generator.

• std::mt19937: random number engine based on the Mersenne Twister algorithm.

• std::uniform_int_distribution: distribution for random integer values between two bounds in a closed interval.

The implementation for the random string generator combining all these features together is shown below:

std::string random_string(std::size_t length)
{
    const std::string CHARACTERS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz";

    std::random_device random_device;
    std::mt19937 generator(random_device());
    std::uniform_int_distribution<> distribution(0, CHARACTERS.size() - 1);

    std::string random_string;

    for (std::size_t i = 0; i < length; ++i)
    {
        random_string += CHARACTERS[distribution(generator)];
    }

    return random_string;
}

As you can see, this function hard codes all the possible characters that will be used to form the random string. Then, it initializes the three needed objects from the Random header by creating a Mersenne Twister engine and a distribution that covers all indexes from the possible characters string. Ultimately, it iterates through the arbitrary length given as a parameter to populate the string with a random character in every iteration.

Conclusion

Avoiding the use of rand() is a piece of advice that does not only apply to create random strings. Instead, it is recommended to use the facilities provided in the Random header that were included in the C++11 Standard Library.

Source Code

How to Split a String in C++

Splitting a string seems like a basic function that any language should have out of the box. Yet, C++ doesn’t provide an in-built method in the standard library that takes care of this task. The reason for the absence of this feature is likely due to the fact that the algorithm has to define the type of container it returns, or that there is a large number of configurations with different parameters that would complicate its interface. To deal with this situation we will implement three different split functions with separate needs in mind.

Split Method #1 (Only Whitespace)
The first implementation for a split function consists of a method that accepts the string to split as its parameter and returns a vector of strings that are delimited by whitespace. This solution makes use of stream iterators to populate the vector with all the tokens in the string.

std::vector<std::string> split(const std::string& string)
{
    std::istringstream i_stream(string);

    return std::vector<std::string>{std::istream_iterator<std::string>{i_stream},
        std::istream_iterator<std::string>()};
}

Split Method #2 (Char Delimeter)
The second implementation accepts a custom delimeter in the form of a character and returns a vector of strings with all tokens. It takes advantage of the getline function that extracts all the characters into a token until the delimeter is found.

std::vector<std::string> split(const std::string& string, char delimeter)
{
    std::stringstream stream(string);

    std::string token;
    std::vector<std::string> tokens;

    while (std::getline(stream, token, delimeter))
    {
        tokens.push_back(token);
    }

    return tokens;
}

Split Method #3 (String Delimeter)
The last method provides an even more general solution that accepts a string delimeter to separate all the tokens. The way it works consists of finding the starting index of each delimeter using the string find function and then extract the token by using the substring method.

std::vector<std::string> split(const std::string& string, const std::string& delimeter)
{
    std::size_t start_index = 0, end_index = 0;

    std::vector<std::string> tokens;

    while ((end_index = string.find(delimeter, start_index)) != std::string::npos)
    {
        auto token = string.substr(start_index, end_index - start_index);
        start_index = end_index + delimeter.size();

        tokens.push_back(token);
    }

    tokens.push_back(string.substr(start_index));

    return tokens;
}

Conclusion

Clearly, the lack of a split function in the standard library can be a cumbersome realization. Luckily, implementing the split algorithm is not a complicated task as it was previously shown in the code snippets. On another note, external libraries such as boost include built-in alternatives for split functionality that remove the need to worry about implementation details.

Source Code

The Spaceship Operator and Its Importance for Class Types in Non-Type Template Parameters

The spaceship operator coming in C++20 was first proposed as a means to simplify the overloading of comparison operators for a specific class. Undoubtedly, it fulfilled its goal as it drastically shortened the code needed to describe each comparison operator(==, !=, <, <=, >, >=).

//Previous C++ code
struct Foo
{
  int x;
  
  friend bool operator==(Foo const& foo1, Foo const& foo2) 
  { return foo1.x == return foo2.x; }
  friend bool operator!=(Foo const& foo1, Foo const& foo2) 
  { return !(foo1 == foo2); }
  friend bool operator< (Foo const& foo1, Foo const& foo2) 
  { return foo1.x < foo2.x; }
  friend bool operator<=(Foo const& foo1, Foo const& foo2) 
  { return !(foo2 < foo1); }
  friend bool operator> (Foo const& foo1, Foo const& foo2)
  { return foo2 < foo1; }
  friend bool operator>=(Foo const& foo1, Foo const& foo2) 
  { return !(foo1 < foo2); }
};

//C++20 Code
struct Foo
{
  int x;
  
  auto operator<=>(Foo const&) = default;
};

This new language feature takes advantage of automatic generation; effectively creating the needed comparison operators without any issues. An important thing to note is that the spaceship operator returns five possible types: std::strong_ordering, std::weak_ordering, std::partial_ordering, std::strong_equality, and std::weak_equality. Each of which follow the following models:

Model	Return Type	Operators
Total order	std::strong_ordering	==, !=, <, <=, >, >=
Weak order	std::weak_ordering	==, !=, <, <=, >, >=
Partial order	std::partial_ordering	==, !=, <, <=, >, >=
Equality comparabe	std::strong_equality	==, !=
Equivalence comparable	std::weak_equality	==, !=

Beyond the clear gains in conciseness, the three-way comparison operator provides a new solution to the existing irregularities for class types in non-type template type parameters; an idea that wasn’t expected by the creator of the spaceship operator proposal(Herb Sutter). The problem with non-type template type parameters is that they currently only accept a small subset of types consisting of integral types, enum types, pointer types, pointer-to-member types, reference types, and std::nullptr_t; which in turn causes an inconsistency in the language by separating the use of certain types for no concrete reason. Removing this inconsistency became apparently hard, until the proposal for the spaceship operator came into fruition.

Integrating the spaceship operator to the language would guarantee equality for different instantiations of a templated entity; effectively letting custom types to be accepted as template type parameters by ensuring the following:

• The class type has a comparison operator.

• The class type has the same comparison operator available in all translation units.

• The class implements member-wise equality.

Conclusion

The spaceship operator not only reduces the code needed to overload comparison operators as it also provides a clear solution to the inconsistencies related to class types in non-type template parameters. For further reading into this topic read the spaceship operator proposal as well as the class types in non-type template parameters proposal.

Concepts: The Next Major Change Coming to C++

The upcoming C++ standard is set to promise many different features and changes that will simplify and expand the way we write and think of code. Upon the wide variety of additions to the language, the inclusion of Concepts tops the list as the most significant one, as they are essential to simplify the use of generic programming. The currently ongoing CppCon has sparked my interest on the topic thanks to the talk given by Bjarne Stroustrup on the future of generic programming. Which covered the importance of concepts in the future of the language as described by the Concepts TS.

What is a Concept?

A Concept is a set of requirements that yield a boolean value at compile-time. They describe the characteristics needed for a certain group of objects to be used inside a template e.g.
Number: - Must provide arithmetic operators(+, +=, -, -=, *, *=, /, /=)
- Must be constructible from 0
- Must be copyable
- Must be movable

Why do we need Concepts?

- Simplify the way we write generic code by removing the verbosity and repetitiveness that templates bring e.g.

//Old C++ template version
template<typename T>
void sort(T& container)
{
    //Sort algorithm
}

//New C++ concept version
void sort(Sortable& container) //Sortable is a concept
{
    //Sort algorithm
}

- Provide more precise and helpful error messages which in the past have been known to daunting and irrelevant e.g.

int a = 42;

//Old error message 
sort(a) // -> error: 'a' doesn't have a [] operator

//New error message with concepts
sort(a) // -> error: 'a' is not Sortable (int doesn't provide [] operator)

- Allow the use of overloads for functions using concepts e. g.

template<RandomAccessIterator Iter>  //RandomAccessIterator is a concept
void distance(Iter first, Iter last)
{
  //Distance Implemnetation for random access iterators
}

template<Iterator Iter> //Iterator is a concept
void distance(Iter first, Iter last)
{
  //Distance implementation for the rest of iterators
}

- Remove the ugliness and complexity coming from the use of enable_if by replacing it with the use of the keyword requires e.g.

//Old code using enable_if
template<typename T>
class Foo
{
  public:
  template<typename U, std::enable_if<std::is_same<T, U>::value && std::is_copy_constructible<U>::value>>
  explicit Foo(const T& object) :
      object(object)
  {}

  private:
  T object;
};

//New code using concepts
template<typename T>
class Foo
{
  public:
  explicit Foo(const T& object)
  requires std::is_copy_constructible<T>::value :
  object(object)
  {}

  private:
  T object;
};

How do we use Concepts?

The first step is to either define a new concept or use an already existing one. Here is an example using the previously mentioned concept of a number:

template<typename T>
concept Number = requires(T a, T b)
{
  { a + b } -> T;
  { a += b } -> T&;
  { a - b } -> T;
  { a -= b } -> T&;
  { a * b } -> T;
  { a *= b } -> T&;
  { a / b } -> T;
  { a /= b } -> T&;
  
  { T{0} };
  
  requires std::is_copy_constructible<T>;
  requires std::is_move_constructible<T>;
}

Then we simply use the already defined concept in a function:

template<Number N>
N pow(N number)
{
  //power exponent implementation
}

Conclusion

Concepts fill in a void that was missing in the language; they effectively improve and simplify the use of generic code. It’s important to understand and appreciate their benefits to start adhering them into our code base as soon as C++20 arrives.